Scheduling Forward Pass Analysis Tutorial
This is a continuation of the SAP BW Best Practice Series on SAP Project Management. In this article I review the Scheduling Forward Pass Analysis technique. As a Project Manager, sooner or later, you will have to consider how you are going to schedule your project and this blog discusses one part of the overall scheduling process.
Avoid Bad Starts With a Forward Pass Analysis
If you are in the middle of development for your next Go-Live or doing an upgrade of an existing SAP BW or Business Objects dashboard system or working on any type of greenfield or ongoing ERP project, I recommend taking a look at this Forward Pass Analysis discussion to avoid a bad start. We have worked with this method and it works fine in the field and we have discovered that what looks to be the obvious schedule in the beginning is not always the correct schedule once a proper analysis has been performed. In this Article, I present Project Forward Pass Analysis practices, a very important and necessary project management planning stage to your overall project success.
FORWARD PASS ANALYSIS
A Forward Pass Analysis is a systematic method of walking through a Work Breakdown Structure (WBS) Network Diagram in order to calculate the Early Start Times and Early Finish Times of each network diagram node element based on estimated WBS Dictionary Element or WBS Task Durations.
The Early Start time (ES) informs the Project Manager how early a task can start. The Early Finish time (EF) informs the Project Manager how early a task is expected to finish given the Task’s expected start time and estimated Duration.
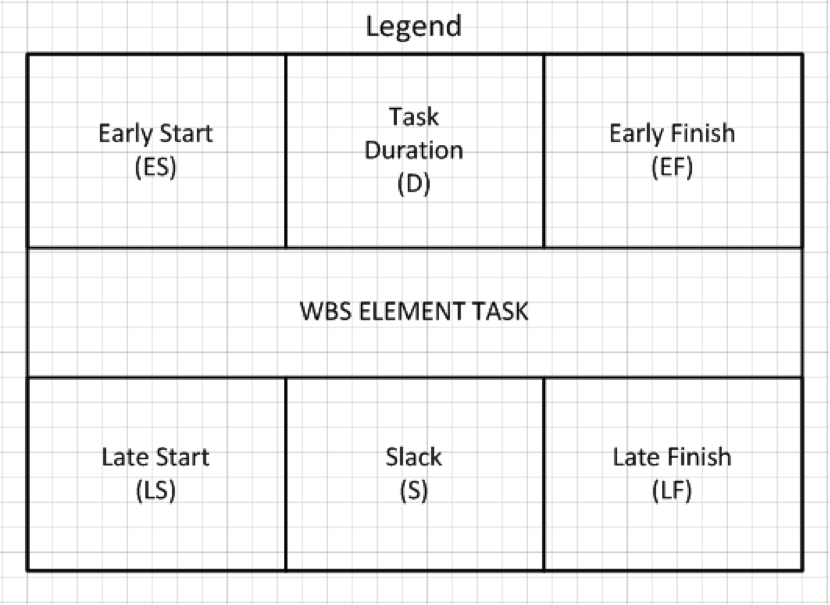
WBS Activity Network Diagram Node Representation
Each WBS Activity Network diagram node can be represented using the following convenient format with the forward pass Early Start (ES), Task Duration (D) and Early Finish (EF) times listed along the top row while the WBS Element Task Name is displayed in the center row and the reverse pass Late Start (LS), Slack (S) and Late Finish (LF) times are listed along the bottom row.

BASIC FORWARD PASS FORMULAS
The basic forward pass Early Start and Early Finish time formulas are as follows:
- Early Finish (task) = Early Start (task) + Duration (task)
- Early Start (next task) = Early Finish (previous task) + 1
It is assumed that each task ends at the close of each business day. However, you can make whatever assumption you want, just make sure you adjust the math accordingly. For this reason, 1 is added to the Early Finish time of the previous task in order to advance the Early Start time of the current task to coincide with the start of the next business day.
The one complication with the forward pass analysis occurs when a task has more than one predecessor activity and we must choose the correct Early Finish time to use in the Early Start calculation. Luckily, we have a rule of thumb that gives us a way out of this conundrum.
FORWARD PASS – RULE OF THUMB
For each node with more than 1 predecessor activity, chose the largest Early Finish time of all connecting predecessor activities.
What this rule of thumb means is that a task has an AND relationship with all predecessor activities.
This AND relationship blocks this task from starting until all predecessor activities have finished. The current task can’t be started until all the dependency tasks have completed.
In order to find the Largest Early Finish time of all connecting predecessor activities, the Project Manager has two options. The first option is to perform two complete forward passes and them make time adjustments according to the rule of thumb.
This results in a second forward pass analysis once the correct predecessor activity time is chosen. In the second option the project manager can simply perform a partial forward pass for all predecessor activity network paths and then apply the rule of thumb. Either method will work fine and gives the same results.
FORWARD PASS – TIME ZERO ELEMENT
The Early Start (ES) time of the first WBS Dictionary Node Element is assumed to be Zero (0) time.
When it becomes time to set up the project schedule, this time zero element will simply be overlaid onto an actual calendar as the project starting point.
FORWARD PASS – GO-HIGH METHOD
When identifying the paths in the Network Diagram, by always traversing from left to right and upward (go-high) along untraveled paths, this is an error free method to ensure that all paths have been identified and that no path has been missed.
The following Sample WBS Activity Network Diagram is repeated here as a reference of our starting point. When finished I will provide the true and correct Project Network Diagram after all the times have been adjusted properly. Notice that this diagram has five special case nodes shown in Red and Green that require special handling.

Sample WBS Activity Network Diagram
HOW TO CALCULATE EARLY START (ES) and EARLY FINISH (EF) TIMES
Now that we have explained the benefits of the Early Start Times and Early Finish Times, covered the basics of the Forward Pass Analysis and provided some useful rules of thumb to keep in mind when performing a forward pass, we will now continue our analysis of the seven project network paths in our sample project starting with Path-1.
PATH-1, FORWARD PASS
Given:
Path-1 = 1.1, 1.2, 1.3, 1.4, 2.2, 2.3, 2.4, 2.5, 3.1, 3.2, 3.3, 3.4, 3.6, 4.2, 4.3
Path-1 = 8 + 128 + 8 + 32 + 40 + 8 + 24 + 8 + 4 + 4 + 4 + 4 + 8 + 8 + 8 = 296 Hours
perform the Forward Pass.
PATH-1, INITIAL CONDITION
First we start with Element 1.1 (moving from left to right). Since WBS Element 1.1 is the first activity and has no predecessor activity the Early Start (ES) time of element 1.1 is defined as zero or ES(1.1) = 0. This is in line with the rule of thumb Forward Pass – Time Zero Element which states The Early Start (ES) time of the first WBS Dictionary Node Element is assumed to be Zero (0) time.
Since we also know from the WBS dictionary, the estimated duration (D) of element 1.1 is 8 hours we can now calculate the Early Finish (EF) time of element 1.1 to be EF(1.1) = Early Start(1.1)+ Duration(1.1) = ES(1.1) + D(1.1)= 8 + 0 = 8 hours. The following diagram summarizes our results for WBS Element Task (1.1).

Moving to element 1.2, we see element 1.2 cannot start until element 1.1 has finished (it has a dependent predecessor activity) and that element 1.1 is the only predecessor with a duration of 8 hours, so WBS Element (1.2) will start on hour 9.
The Early Start of Element ES(1.2) = EF(1.1) + 1 = 9 and the Early Finish of Element 1.2 = ES(1.2) + Duration (1.2) = 9 + 128 = 137.
Completing the forward pass exercise for all the other elements in Path-1, we get the following Forward Pass analysis results:
1) Element 1.1: ES(1.1) = 0,
2) EF(1.1) = ES(1.1) + D(1.1) = 0 + 8 = 8
3)
4) Element 1.2: ES(1.2) = EF(1.1) + 1 = 8 + 1 = 9
5) EF(1.2) = ES(1.2) + D(1.2) = 9 + 128 = 137
6)
7) Element 1.3: ES(1.3) = EF(1.2) + 1 = 138
8) EF(1.3) = ES(1.3) + D(1.3) = 138 + 8 = 146
9)
10) Element 1.4: ES(1.4) = EF(1.3) + 1 = 147
11) EF(1.4) = ES(1.4) + D(1.4) = 147 + 32 = 179
12)
13) Element 2.2: ES(2.2) = EF(1.4) + 1 = 180
14) EF(2.2) = ES(2.2) + D(2.2) = 180 + 40 = 220
15)
16) Element 2.3: ES(2.3) = EF(2.2) + 1 = 221
17) EF(2.3) = ES(2.3) + D(2.3) = 221 + 8 = 229
18)
19) Element 2.4: ES(2.4) = EF(2.3) + 1 = 230
20) EF(2.4) = ES(2.4) + D(2.4) = 230 + 24 = 254
21)
22) Element 2.5: ES(2.5) = EF(2.4) + 1 = 255
23) EF(2.5) = ES(2.5) + D(2.5) = 255 + 8 = 263
24)
25) Element 3.1: ES(3.1) = EF(2.5) + 1 = 264
26) EF(3.1) = ES(3.1) + D(3.1) = 264 + 4 = 268
27)
28) Element 3.2: ES(3.2) = EF(3.1) + 1 = 269
29) EF(3.2) = ES(3.2) + D(3.2) = 269 + 4 = 273
30)
31) Element 3.3: ES(3.3) = EF(3.2) + 1 = 274
32) EF(3.3) = ES(3.3) + D(3.3) = 274 + 4 = 278
33)
34) Element 3.4: ES(3.4) = EF(3.3) + 1 = 279
35) EF(3.4) = ES(3.4) + D(3.4) = 279 + 4 = 283
36)
37) Element 3.6: ES(3.6) = EF(3.4) + 1 = 284
38) EF(3.6) = ES(3.6) + D(3.6) = 284 + 8 = 292
39)
40) Element 4.2: ES(4.2) = EF(3.6) + 1 = 293
41) EF(4.2) = ES(4.2) + D(4.2) = 293 + 8 = 301
42)
43) Element 4.3: ES(4.3) = EF(4.2) + 1 = 302
44) EF(4.3) = ES(4.3) + D(4.3) = 302 + 8 = 310
This is the results of the initial forward pass for Path-1. We can see from the sequence diagram that WBS Element (2.4) and WBS Element (3.6) have more than 1 predecessor activity. For this reason, we cannot completely analyze Path-1 until we have completed the forward pass for all predecessor activities to Elements 2.4 and 3.6. Once we have those partial forward pass results, we can then adjust the Early Start times of Elements 2.4 and 3.6 and then complete the Forward Pass Path-1 analysis. Once that is done, we can then repeat the same processes with Path-2 through Path-7.
PATH-2, FORWARD PASS
Given:
Path-2 = 1.1, 1.2, 1.3, 1.5, 2.4, 2.5, 3.1, 3.2, 3.3, 3.4, 3.6, 4.2, 4.3
Path-2 Durations = 8 + 128 + 8 + 32 + 24 + 8 + 4 + 4 + 4 + 4 + 8 + 8 + 8 = 248 Hours
Perform the Forward Pass.
We get the following Forward Pass analysis results for Path-2:
1) Element 1.1: ES(1.1) = 0
2) EF(1.1) = ES(1.1) + D(1.1) = 0 + 8 = 8
3)
4) Element 1.2: ES(1.2) = EF(1.1) + 1 = 8 + 1=9
5) EF(1.2) = ES(1.2) + D(1.2) = 9 + 128 = 137
6)
7) Element 1.3: ES(1.3) = EF(1.2) + 1 = 138
8) EF(1.3) = ES(1.3) + D(1.3) = 138 + 8 = 146
9)
10) Element 1.5: ES(1.5) = EF(1.3) + 1 = 147
11) EF(1.5) = ES(1.5) + D(1.5) = 147 + 32 = 179
12)
13) Element 2.4: ES(2.4) = EF(1.5) + 1 = 180
14) EF(2.4) = ES(2.4) + D(2.4) = 180 + 24 = 204
15)
16) Element 2.5: ES(2.5) = EF(2.4) + 1 = 205
17) EF(2.5) = ES(2.5) + D(2.5) = 205 + 8 = 213
18)
19) Element 3.1: ES(3.1) = EF(2.5) + 1 = 214
20) EF(3.1) = ES(3.1) + D(3.1) = 214 + 4 = 218
21)
22) Element 3.2: ES(3.2) = EF(3.1) + 1 = 219
23) EF(3.2) = ES(3.2) + D(3.2) = 219 + 4 = 223
24)
25) Element 3.3: ES(3.3) = EF(3.2) + 1 = 224
26) EF(3.3) = ES(3.3) + D(3.3) = 224 + 4 = 228
27)
28) Element 3.4: ES(3.4) = EF(3.3) + 1 = 229
29) EF(3.4) = ES(3.4) + D(3.4) = 229 + 4 = 233
30)
31) Element 3.6: ES(3.6) = EF(3.4) + 1 = 234
32) EF(3.6) = ES(3.6) + D(3.6) = 234 + 8 = 242
33)
34) Element 4.2: ES(4.2) = EF(3.6) + 1 = 243
35) EF(4.2) = ES(4.2) + D(4.2) = 243 + 8 = 251
36)
37) Element 4.3: ES(4.3) = EF(4.2) + 1 = 252
38) EF(4.3) = ES(4.3) + D(4.3) = 252 + 8 = 260
39)
PATH-3, FORWARD PASS
Given:
Path-3 = 1.1, 1.2, 1.3, 1.6, 2.4, 2.5, 3.1, 3.2, 3.3, 3.4, 3.6, 4.2, 4.3
Path-3 Durations = 8 + 128 + 8 + 4 + 24 + 8 + 4 + 4 + 4 + 4 + 8 + 8 + 8 = 220 Hours
perform the Forward Pass.
We get the following Forward Pass analysis results for Path-3:
1) Element 1.1: ES(1.1) = 0,
2) EF(1.1) = ES(1.1) + D(1.1) = 0 + 8 = 8
3)
4) Element 1.2: ES(1.2) = EF(1.1) + 1 = 8 + 1=9
5) EF(1.2) = ES(1.2) + D(1.2) = 9 + 128 = 137
6)
7) Element 1.3: ES(1.3) = EF(1.2) + 1 = 138
8) EF(1.3) = ES(1.3) + D(1.3) = 138 + 8 = 146
9)
10) Element 1.6: ES(1.6) = EF(1.3) + 1 = 147
11) EF(1.6) = ES(1.6) + D(1.6) = 147 + 4 = 151
12)
13) Element 2.4: ES(2.4) = EF(1.6) + 1 = 152
14) EF(2.4) = ES(2.4) + D(2.4) = 152 + 24 = 176
15)
16) Element 2.5: ES(2.5) = EF(2.4) + 1 = 177
17) EF(2.5) = ES(2.5) + D(2.5) = 177 + 8 = 185
18)
19) Element 3.1: ES(3.1) = EF(2.5) + 1 = 186
20) EF(3.1) = ES(3.1) + D(3.1) = 186 + 4 = 190
21)
22) Element 3.2: ES(3.2) = EF(3.1) + 1 = 191
23) EF(3.2) = ES(3.2) + D(3.2) = 191 + 4 = 195
24)
25) Element 3.3: ES(3.3) = EF(3.2) + 1 = 196
26) EF(3.3) = ES(3.3) + D(3.3) = 196 + 4 = 200
27)
28) Element 3.4: ES(3.4) = EF(3.3) + 1 = 201
29) EF(3.4) = ES(3.4) + D(3.4) = 201 + 4 = 205
30)
31) Element 3.6: ES(3.6) = EF(3.4) + 1 = 206
32) EF(3.6) = ES(3.6) + D(3.6) = 206 + 8 = 214
33)
34) Element 4.2: ES(4.2) = EF(3.6) + 1 = 215
35) EF(4.2) = ES(4.2) + D(4.2) = 215 + 8 = 223
36)
37) Element 4.3: ES(4.3) = EF(4.2) + 1 = 224
38) EF(4.3) = ES(4.3) + D(4.3) = 224 + 8 = 232
39)
PATH-4, FORWARD PASS
Given:
Path-4 = 1.1, 1.2, 1.3, 2.1, 2.4, 2.5, 3.1, 3.2, 3.3, 3.4, 3.6, 4.2, 4.3
Path-4 Durations = 8 + 128 + 8 + 4 + 24 + 8 + 4 + 4 + 4 + 4 + 8 + 8 + 8 = 220 Hours
Perform the Forward Pass.
We get the following Forward Pass analysis results for Path-4:
1) Element 1.1: ES(1.1) = 0,
2) EF(1.1) = ES(1.1) + D(1.1) = 0 + 8 = 8
3)
4) Element 1.2: ES(1.2) = EF(1.1) + 1 = 8 + 1=9
5) EF(1.2) = ES(1.2) + D(1.2) = 9 + 128 = 137
6)
7) Element 1.3: ES(1.3) = EF(1.2) + 1 = 138
8) EF(1.3) = ES(1.3) + D(1.3) = 138 + 8 = 146
9)
10) Element 2.1: ES(2.1) = EF(1.3) + 1 = 147
11) EF(2.1) = ES(2.1) + D(2.1) = 147 + 4 = 151
12)
13) Element 2.4: ES(2.4) = EF(2.1) + 1 = 152
14) EF(2.4) = ES(2.4) + D(2.4) = 152 + 24 = 176
15)
16) Element 2.5: ES(2.5) = EF(2.4) + 1 = 177
17) EF(2.5) = ES(2.5) + D(2.5) = 177 + 8 = 185
18)
19) Element 3.1: ES(3.1) = EF(2.5) + 1 = 186
20) EF(3.1) = ES(3.1) + D(3.1) = 186 + 4 = 190
21)
22) Element 3.2: ES(3.2) = EF(3.1) + 1 = 191
23) EF(3.2) = ES(3.2) + D(3.2) = 191 + 4 = 195
24)
25) Element 3.3: ES(3.3) = EF(3.2) + 1 = 196
26) EF(3.3) = ES(3.3) + D(3.3) = 196 + 4 = 200
27)
28) Element 3.4: ES(3.4) = EF(3.3) + 1 = 201
29) EF(3.4) = ES(3.4) + D(3.4) = 201 + 4 = 205
30)
31) Element 3.6: ES(3.6) = EF(3.4) + 1 = 206
32) EF(3.6) = ES(3.6) + D(3.6) = 206 + 8 = 214
33)
34) Element 4.2: ES(4.2) = EF(3.6) + 1 = 215
35) EF(4.2) = ES(4.2) + D(4.2) = 215 + 8 = 223
36)
37) Element 4.3: ES(4.3) = EF(4.2) + 1 = 224
38) EF(4.3) = ES(4.3) + D(4.3) = 224 + 8 = 232
39)
PATH-5, FORWARD PASS
Given:
Path-5 = 1.1, 1.2, 1.3, 2.6, 2.4, 2.5, 3.1, 3.2, 3.3, 3.4, 3.6, 4.2, 4.3
Path-5 Durations = 8 + 128 + 8 + 8 + 24 + 8 + 4 + 4 + 4 + 4 + 8 + 8 + 8 = 224 Hours
Perform the Forward Pass.
We get the following Forward Pass analysis results for Path-5:
1) Element 1.1: ES(1.1) = 0,
2) EF(1.1) = ES(1.1) + D(1.1) = 0 + 8 = 8
3)
4) Element 1.2: ES(1.2) = EF(1.1) + 1 = 8 + 1=9
5) EF(1.2) = ES(1.2) + D(1.2) = 9 + 128 = 137
6)
7) Element 1.3: ES(1.3) = EF(1.2) + 1 = 138
8) EF(1.3) = ES(1.3) + D(1.3) = 138 + 8 = 146
9)
10) Element 2.6: ES(2.6) = EF(1.3) + 1 = 147
11) EF(2.6) = ES(2.6) + D(2.6) = 147 + 8 = 155
12)
13) Element 2.4: ES(2.4) = EF(2.6) + 1 = 155
14) EF(2.4) = ES(2.4) + D(2.4) = 155 + 24 = 179
15)
16) Element 2.5: ES(2.5) = EF(2.4) + 1 = 180
17) EF(2.5) = ES(2.5) + D(2.5) = 180 + 8 = 188
18)
19) Element 3.1: ES(3.1) = EF(2.5) + 1 = 189
20) EF(3.1) = ES(3.1) + D(3.1) = 189 + 4 = 193
21)
22) Element 3.2: ES(3.2) = EF(3.1) + 1 = 194
23) EF(3.2) = ES(3.2) + D(3.2) = 194 + 4 = 198
24)
25) Element 3.3: ES(3.3) = EF(3.2) + 1 = 199
26) EF(3.3) = ES(3.3) + D(3.3) = 199 + 4 = 203
27)
28) Element 3.4: ES(3.4) = EF(3.3) + 1 = 204
29) EF(3.4) = ES(3.4) + D(3.4) = 204 + 4 = 208
30)
31) Element 3.6: ES(3.6) = EF(3.4) + 1 = 209
32) EF(3.6) = ES(3.6) + D(3.6) = 209 + 8 = 217
33)
34) Element 4.2: ES(4.2) = EF(3.6) + 1 = 218
35) EF(4.2) = ES(4.2) + D(4.2) = 218 + 8 = 226
36)
37) Element 4.3: ES(4.3) = EF(4.2) + 1 = 227
38) EF(4.3) = ES(4.3) + D(4.3) = 227 + 8 = 235
PATH-6, FORWARD PASS
Given:
Path-6 = 1.1, 1.2, 3.5, 3.6, 4.2, 4.3
Path-6 Durations = 8 + 128 + 4 + 8 + 8 + 8 = 164 Hours
Perform the Forward Pass.
We get the following Forward Pass analysis results for Path-6:
1) Element 1.1: ES(1.1) = 0,
2) EF(1.1) = ES(1.1) + D(1.1) = 0 + 8 = 8
3)
4) Element 1.2: ES(1.2) = EF(1.1) + 1 = 8 + 1=9
5) EF(1.2) = ES(1.2) + D(1.2) = 9 + 128 = 137
6)
7) Element 3.5: ES(3.5) = EF(1.2) + 1 = 138
8) EF(3.5) = ES(3.5) + D(3.5) = 138 + 4 = 142
9)
10) Element 3.6: ES(3.6) = EF(3.5) + 1 = 143
11) EF(3.6) = ES(3.6) + D(3.6) = 143 + 8 = 151
12)
13) Element 4.2: ES(4.2) = EF(3.6) + 1 = 152
14) EF(4.2) = ES(4.2) + D(4.2) = 152 + 8 = 160
15)
16) Element 4.3: ES(4.3) = EF(4.2) + 1 = 161
17) EF(4.3) = ES(4.3) + D(4.3) = 161 + 8 = 169
18)
Finally we reach Path-7.
PATH-7, FORWARD PASS
Given:
Path-7 = 1.1, 1.2, 4.1, 3.5, 3.6, 4.2, 4.3
Path-7 Durations = 8 + 128 + 120 + 4 + 8 + 8 + 8 = 284 Hours
Perform the Forward Pass.
We get the following Forward Pass analysis results for Path-7:
1) Element 1.1: ES(1.1) = 0,
2) EF(1.1) = ES(1.1) + D(1.1) = 0 + 8 = 8
3)
4) Element 1.2: ES(1.2) = EF(1.1) + 1 = 8 + 1=9
5) EF(1.2) = ES(1.2) + D(1.2) = 9 + 128 = 137
6)
7) Element 4.1: ES(4.1) = EF(1.2) + 1 = 138
8) EF(4.1) = ES(4.1) + D(4.1) = 138 +120 = 258
9)
10) Element 3.5: ES(3.5) = EF(4.1) + 1 = 259
11) EF(3.5) = ES(3.5) + D(3.5) = 259 + 4 = 263
12)
13) Element 3.6: ES(3.6) = EF(3.5) + 1 = 264
14) EF(3.6) = ES(3.6) + D(3.6) = 264 + 8 = 272
15)
16) Element 4.2: ES(4.2) = EF(3.6) + 1 = 273
17) EF(4.2) = ES(4.2) + D(4.2) = 273 + 8 = 281
18)
19) Element 4.3: ES(4.3) = EF(4.2) + 1 = 282
20) EF(4.3) = ES(4.3) + D(4.3) = 282 + 8 = 290
21)
Table 1 summarizes the results of the first pass through the Forward Pass.
|
WBS Element Code |
Description of Work |
WBS Element Code Dependencies |
Estimated Time Hrs (Duration) |
Forward Pass One |
|
|
Early Start (ES) |
Early Finish (EF) |
||||
|
1.0 |
|
|
|
|
|
|
1.1 |
Task A |
None |
8 |
0 |
8 |
|
1.2 |
Task B |
1.1 |
128 |
9 |
137 |
|
1.3 |
Task C |
1.2 |
8 |
138 |
146 |
|
1.4 |
Task D |
1.3 |
32 |
147 |
179 |
|
1.5 |
Task E |
1.3 |
32 |
147 |
179 |
|
1.6 |
Task F |
1.3 |
4 |
147 |
151 |
|
2.0 |
|
|
|
|
|
|
2.1 |
Task G |
1.3 |
4 |
147 |
151 |
|
2.2 |
Task H |
1.4 |
40 |
180 |
220 |
|
2.3 |
Task I |
2.2 |
8 |
221 |
229 |
|
2.4 |
Task J |
2.3, 1.5, 1.6, 2.1, 2.6 |
24 |
230 |
254 |
|
2.5 |
Task K |
2.4 |
8 |
255 |
263 |
|
2.6 |
Task L |
1.3 |
8 |
147 |
155 |
|
3.0 |
|
|
|
|
|
|
3.1 |
Task M |
2.5 |
4 |
264 |
268 |
|
3.2 |
Task N |
3.1 |
4 |
269 |
273 |
|
3.3 |
Task O |
3.2 |
4 |
274 |
278 |
|
3.4 |
Task P |
3.3 |
4 |
279 |
283 |
|
3.5 |
Task Q |
1.2, 4.1 |
4 |
138 |
142 |
|
3.6 |
Task R |
3.5, 3.4 |
8 |
284 |
292 |
|
4.0 |
|
|
|
|
|
|
4.1 |
Task S |
1.2 |
120 |
138 |
258 |
|
4.2 |
Task T |
3.6 |
8 |
293 |
301 |
|
4.3 |
Task U |
4.2 |
8 |
302 |
310 |
|
Total |
|
|
468 hours |
|
|
Table 1.
Special Cases, Adjusting the Forward Pass times.
The following chart shows the unadjusted First Pass, Early Finish (EF) times for each node element.

We can see that Element (2.4), Element (3.5) and Element (3.6) each have more than one predecessor activities. These three elements require a second Forward Pass to properly adjust their Early Start and Early Finish times.
Element (2.4) Special Case
Element (2.4) has five connecting predecessor activities:
- Element (2.3) on Path-1 with an Early Finish Time of 229
- Element (1.5) on Path-2 with an Early Finish time of 179
- Element (1.6) on Path-3 with an Early Finish time of 151
- Element (2.1) on Path-4 with an Early Finish time of 151
- Element (2.6) on Path-6 with an Early Finish time of 155
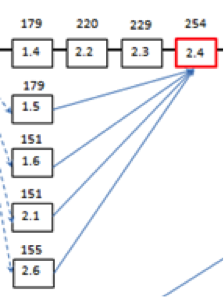
Referring to the RULE that says : For each node with more than 1 predecessor activity, when selecting the Early Start (ES) time for that node, choose the largest Early Finish time of all connecting predecessor activities.
Since Element (2.3) has the largest Early Finish Time of 229, then 229+1 = 230 is the correct Early Start Time to use for Element(2.4).
Element (3.5) Special Case
Element(3.5) has two predecessor activities:
- Element (1.2) on Path-1 with an Early Finish Time of 137
- Element (4.1) on Path-7 with an Early Finish time of 258
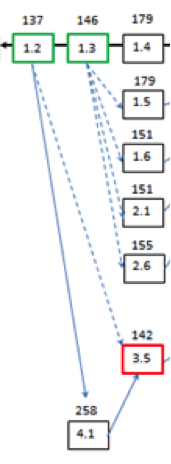
Referring to the RULE that says : For each node with more than 1 predecessor activity, when selecting the Early Start (ES) time for that node, choose the largest Early Finish time of all connecting predecessor activities.
Since Element (4.1) has the largest Early Finish Time of 258, then 258+1 = 259 is the correct Early Start Time to use for Element(3.5) resulting in a new Early Finish time of Element (3.5) = 263.
Element (3.6) Special Case
Element(3.6) has two predecessor activities:
- Element (3.4) on Path-1 with an Early Finish Time of 283
- Element (3.5) on Path-5 with an Early Finish time of 263


Referring to the RULE that says : For each node with more than 1 predecessor activity, when selecting the Early Start (ES) time for that node, choose the largest Early Finish time of all connecting predecessor activities.
Since Element (3.4) has the largest Early Finish Time of 283, then 283+1 = 284 is the correct Early Start Time to use for Element(3.6) with an Early Finish time of Element(3.6) of 292.
To complete the forward pass analysis, it is necessary to go through all seven paths and to make time adjustments as we have done with Path-1. The following chart and table summarizes the final Forward Pass results for all 7 Project WBS Network Diagram Nodes.

Completed WBS Network Diagram after completing the Forward Pass Analysis
We can also summarize and update the results of the Forward Pass Analysis in the WBS Dictionary.
|
WBS Element Code |
Description of Work |
WBS Element Code Dependencies |
Estimated Time Hrs (Duration) |
Forward Pass |
Reverse Pass |
||
|
Early Start (ES) |
Early Finish (EF) |
Late Start (LS) |
Late Finish (LF) |
||||
|
1.0 |
|
|
|
|
|
|
|
|
1.1 |
Task A |
None |
8 |
0 |
8 |
|
|
|
1.2 |
Task B |
1.1 |
128 |
9 |
137 |
|
|
|
1.3 |
Task C |
1.2 |
8 |
138 |
146 |
|
|
|
1.4 |
Task D |
1.3 |
32 |
147 |
179 |
|
|
|
1.5 |
Task E |
1.3 |
32 |
147 |
179 |
|
|
|
1.6 |
Task F |
1.3 |
4 |
147 |
151 |
|
|
|
2.0 |
|
|
|
|
|
|
|
|
2.1 |
Task G |
1.3 |
4 |
147 |
151 |
|
|
|
2.2 |
Task H |
1.4 |
40 |
180 |
220 |
|
|
|
2.3 |
Task I |
2.2 |
8 |
221 |
229 |
|
|
|
2.4 |
Task J |
2.3, 1.5, 1.6, 2.1, 2.6 |
24 |
230 |
254 |
|
|
|
2.5 |
Task K |
2.4 |
8 |
255 |
263 |
|
|
|
2.6 |
Task L |
1.3 |
8 |
147 |
155 |
|
|
|
3.0 |
|
|
|
|
|
|
|
|
3.1 |
Task M |
2.5 |
4 |
264 |
268 |
|
|
|
3.2 |
Task N |
3.1 |
4 |
269 |
273 |
|
|
|
3.3 |
Task O |
3.2 |
4 |
274 |
278 |
|
|
|
3.4 |
Task P |
3.3 |
4 |
279 |
283 |
|
|
|
3.5 |
Task Q |
1.2, 4.1 |
4 |
259 |
263 |
|
|
|
3.6 |
Task R |
3.5, 3.4 |
8 |
284 |
292 |
|
|
|
4.0 |
|
|
|
|
|
|
|
|
4.1 |
Task S |
1.2 |
120 |
138 |
258 |
|
|
|
4.2 |
Task T |
3.6 |
8 |
293 |
301 |
|
|
|
4.3 |
Task U |
4.2 |
8 |
302 |
310 |
|
|
|
Total |
|
|
468 hours |
|
|
|
|
This concludes the explanation of the forward pass. From the above table, we can see that the 2 columns for the reverse pass are blank. The reverse pass will be the topic of the next blog where we start where we have left off with the Forward Pass and then work our way backwards through the network diagram to calculate the Late Start and Late Finish times of each WBS Node Element.
If you want to find out additional information related to successfully managing a SAP project, we have a series of experience based guides you can get for FREE, by clicking the button below.
Thanks